素数平时用到不太多,但技术面试过程中,算法是必不或缺的一环,而斐波那契数列、素数等算法的白板考核较为常见,今天就用 Python 写几个和素数有关的例子吧。
什么是素数?
素数(prime number)又称质数,有无限个。素数定义为在大于1的自然数中,除了1和它本身以外不再有其他因数。
如何判断 n 是否为素数
思路:由素数定义可知,最小的素数是 2。那么最容易想到的判断方法就是,从 2 开始遍历到 n - 1, 判断每个数是否整除 n, 即 n % i == 0, 满足条件则不是素数。
穷举法实现:
1 | # 复杂度 O(n) |
优化穷举法(1)
复盘:很明显执行时间会很长,主要是穷举法的遍历范围太广,可以考虑缩减遍历范围入手优化。
启发:中学数据的因式分解可以给出一些启发,即如果一个数可以因式分解,那分解得到的两个数,必定一个小于等于 sqrt(n), 一个大于等于 sqrt(n)。(sqrt表示开方函数)
思路:判断 n 是否素数不需要遍历到 n-1,遍历到 sqrt(n) 即可,因为若 sqrt(n) 左侧找不到约数,那么右侧也一定找不到。
实现:
1 | # 复杂度 O(√n) |
优化穷举法(2)
复盘:开方法使得遍历范围大大缩小,那还有没有优化空间?仔细观察可以发现,对遍历次数影响的因素,除了范围还有步长。上面两种方法的遍历步长均为1,增大步长,遍历次数也会成倍减少。
启发:素数分布存在一个规律,即大于等于5的质数一定和6的倍数相邻。这意味步长可以增大到6,进而判断每个数是否整除 n 或 n+2,即 n % i == 0 or n % (i + 2) == 0, 满足条件则不是素数。
实现:
1 | # 执行时间比开方法小3倍左右,数据量越大,效果越明显 |
执行时间测试
- 测试结果
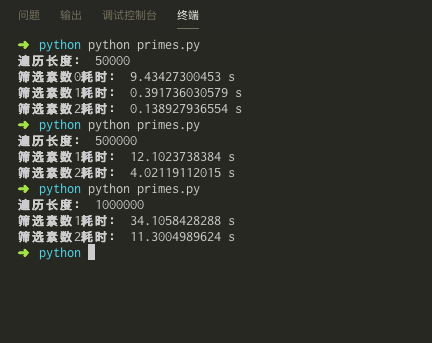
- 测试代码
1 | #!/usr/bin/python |
实践拓展
考题:筛选出小于n内的所有素数
思路:上面已经知道如何高效判断素数了,那么如果高效的筛选出所有素数呢?
启发:有一个更为高效的算法,埃拉托斯特尼筛选法。
原理:埃拉托斯特尼筛法是指,要得到自然数n以内的全部素数,必须把不大于根号n的所有素数的倍数剔除,剩下的都是素数。
说明:简单推理下,最小素数为2,那就把小于等于根号 n 的所有2的倍数剔除,次最小素数为3,把小于等于根号 n 的所有3的倍数剔除,依次类推,最后得到的就是素数。
实现:
1 |
|