因为有 Python 编程基础,数学方面还没有完全还给老师,年前加入FE 的 AI 学习小组,开始学习吴恩达老师的DeepLearning课程,记个笔记、画个重点,总结一下,也方便和增强自己对该课程的进一步学习和理解。
理清神经网络的基础
感知机
感知器(英语:Perceptron)是Frank Rosenblatt在1957年就职于康奈尔航空实验室(Cornell Aeronautical Laboratory)时所发明的一种人工神经网络。它可以被视为一种最简单形式的前馈神经网络,是一种二元线性分类器。
Frank Rosenblatt给出了相应的感知机学习算法,常用的有感知机学习、最小二乘法和梯度下降法。譬如,感知机利用梯度下降法对损失函数进行极小化,求出可将训练数据进行线性划分的分离超平面,从而求得感知机模型。
生物学-神经细胞
神经细胞结构示意图
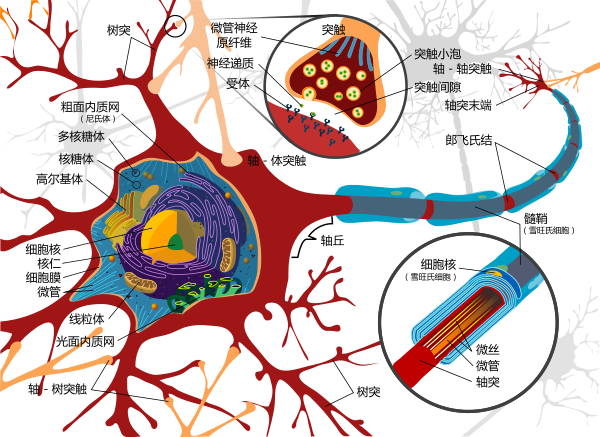
感知机是生物神经细胞的简单抽象。神经细胞结构大致可分为:树突、突触、细胞体及轴突。单个神经细胞可被视为一种只有两种状态的机器——激动时为‘是’,而未激动时为‘否’。神经细胞的状态取决于从其它的神经细胞收到的输入信号量,及突触的强度(抑制或加强)。当信号量总和超过了某个阈值时,细胞体就会激动,产生电脉冲。电脉冲沿着轴突并通过突触传递到其它神经元。为了模拟神经细胞行为,与之对应的感知机基础概念被提出,如权量(突触)、偏置(阈值)及激活函数(细胞体)。
人工神经元
神经元结构示意图
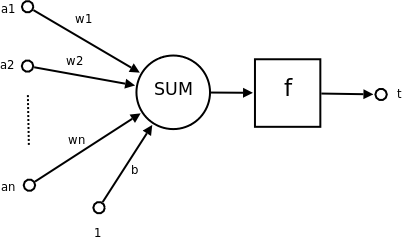
在人工神经网络领域中,感知机也被指为单层的人工神经网络,以区别于较复杂的多层感知机(Multilayer Perceptron)。作为一种线性分类器,(单层)感知机可说是最简单的前向人工神经网络形式。尽管结构简单,感知机能够学习并解决相当复杂的问题。感知机主要的本质缺陷是它不能处理线性不可分问题。
以上内容摘自维基百科
单层感知机的适用和缺陷
适合解决线性问题,如下图
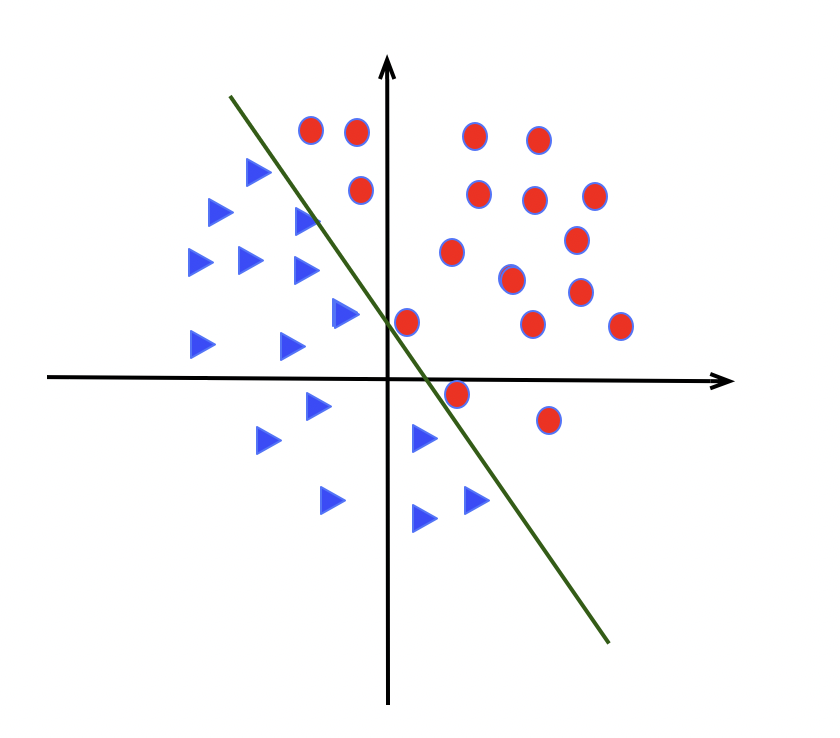
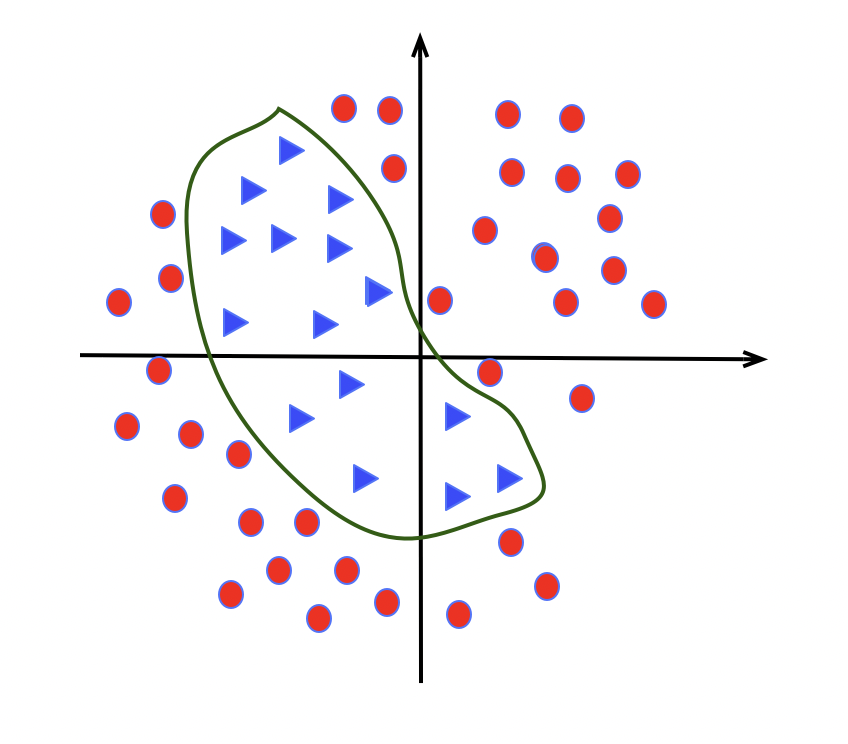
无法解决线性不可分,如常见的 XOR 异或问题,如下图
二分类
目前工业界最能产生价值的是机器学习中的监督学习, 场景有推荐系统,反欺系统诈等等。其中二分类算法应用的尤其之多。

例如上面的图像识别场景, 我们希望判断图片中是否有猫,于是我们为模型输入一张图片,得出一个预测值y。 y的取值为1或者0. 0 代表是,1代表否。
逻辑回归模型
逻辑回归是一个用于二分类(binary classification)的算法。
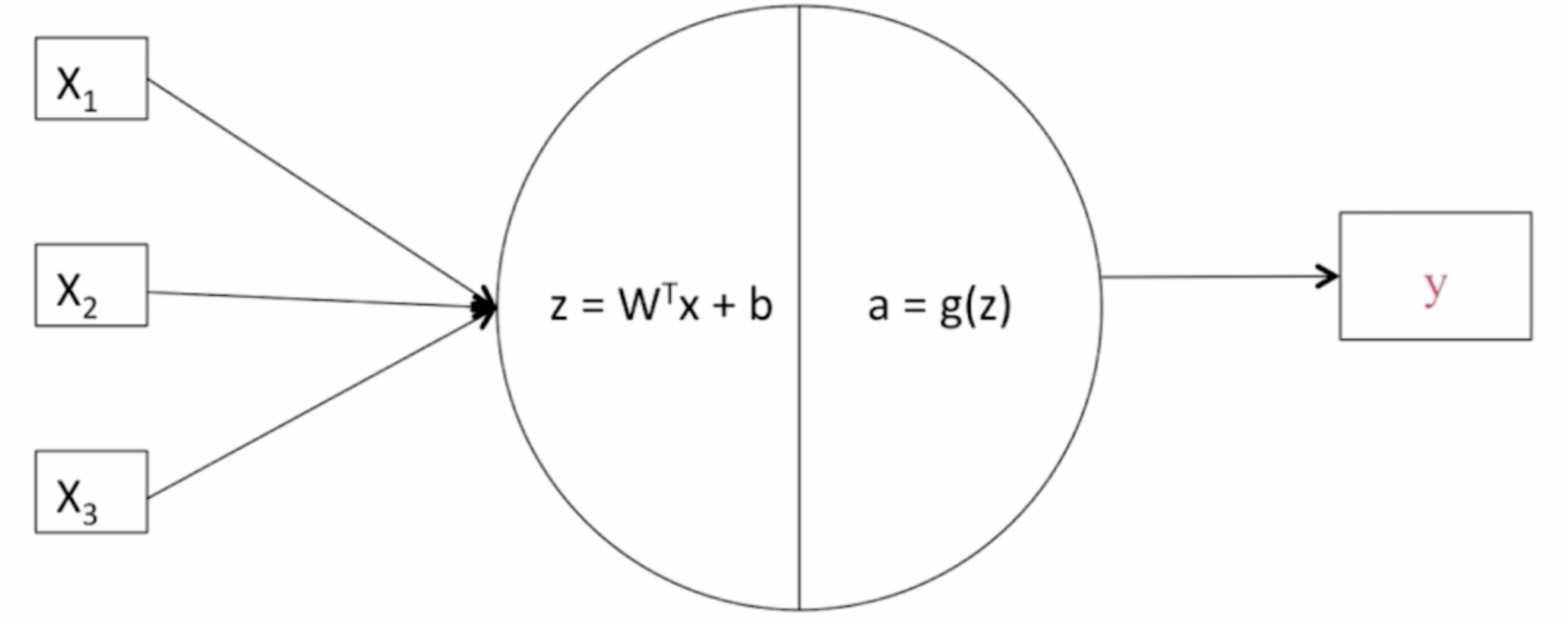
逻辑回归的Hypothesis Function(假设函数)
假设函数: $\Large{\hat{y} = w^Tx + b}$
$\hat{y}$表示$y$等于1的一种可能性或者是机会,前提条件是给定了输入特征$X$。
$w$表示逻辑回归的参数,这也是一个$n_x$维向量(因为$w$实际上是特征权重,维度与特征向量相同)
参数里面还有$b$,这是一个实数(表示偏差)
事实上,$\hat{y} = w^Tx + b$这个线性函数对于二元分类问题不是一个太好的算法,因为$w^Tx + b$可能比1要大得多,或者是个负值。这是个需要解决的问题。
sigmoid函数
sigmoid函数的公式: $\Large{\sigma{(z)} = \frac{1}{1 + e^{-z}} }$
为了解决这个问题,需要将$w^Tx + b$作为sigmoid函数的一个自变量$z$, 用$z$来表示$w^Tx + b$的值,$z = w^Tx + b$,将线性函数转化为非线性函数。所以 $\hat{y} = \sigma{(w^Tx + b)}$相当于$\hat{y} = \sigma{(z)}$
根据$\hat{y}$在$(0,1)$推导出$\sigma{(z)}$的范围也在$(0,1)$
当 z 是个绝对值非常大的负数时,$e^{-z}$会变得非常大,1 除以一个非常大的数加1,$\sigma{(z)}$, 即 $ \frac{1}{1 + e^{-z}} $,会接近于 0
- 当 z 是个绝对值非常大的正数时,$e^{-z}$会变得非常小,接近于0,此时 $ \frac{1}{1 + e^{-z}} $接近于 1
逻辑回归的输出函数
$\Large{\hat{y}^{(i)} = \sigma{(w^Tx^{(i)} + b)}}$, where ${\sigma{(z)} = \frac{1}{1+e^{-z}}}$
$\Large{Given {(x^{(1)},y^{(1)}),…,(x^{(m)},y^{(m)})}}$, want ${\hat{y}^{(i)} \approx y^{(i)}}$
为了让模型通过学习调整参数,你需要给予一个𝑚样本的训练集,这会让你在训练集上 找到参数𝑤和参数𝑏,,来得到你的输出。
激活函数
也叫激励函数,是为了能够给神经网络加入一些非线性因素,使得神经网络可以更好地解决较为复杂的问题。
常见的激活函数
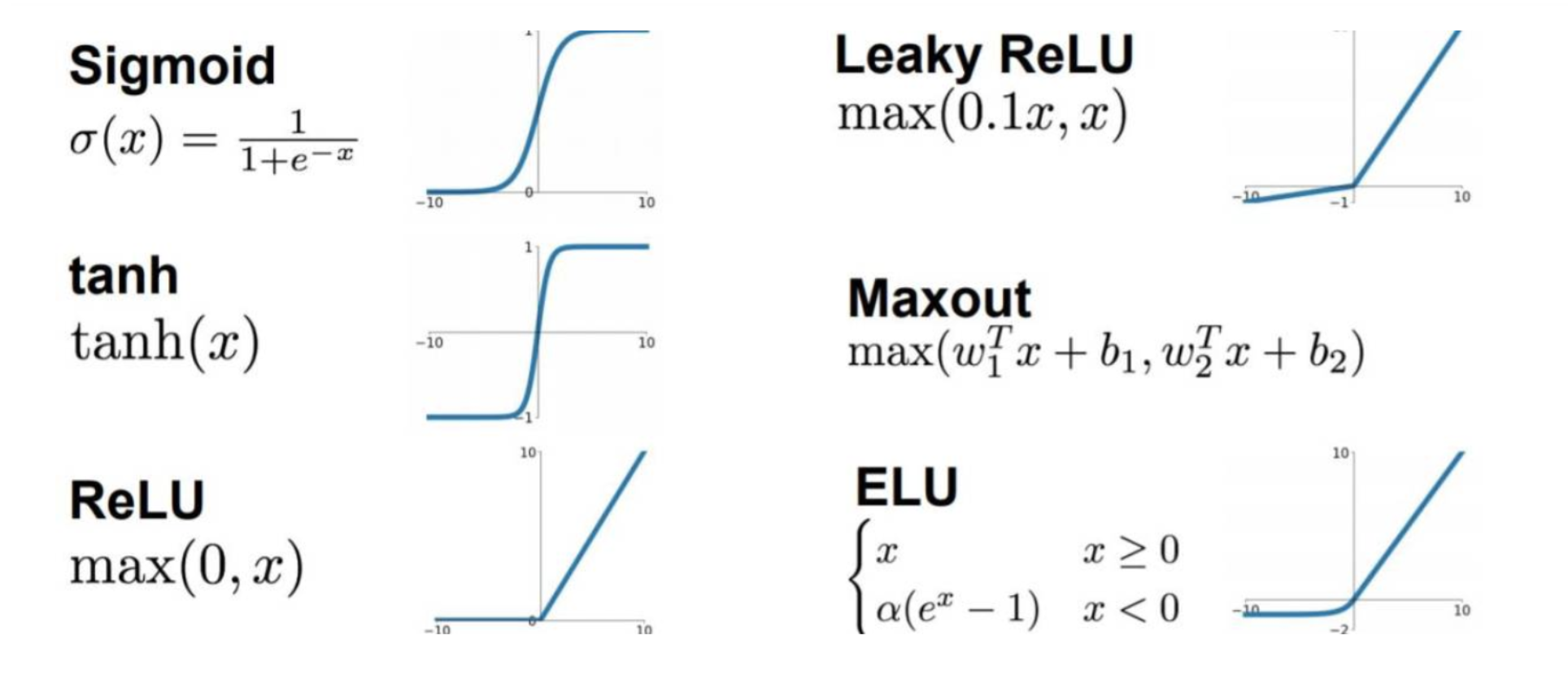
Sigmoid函数
tanh函数
ReLU函数
损失函数(Lost Function)
损失函数又叫做误差函数,用来衡量算法的运行情况,Loss function: $L(\hat{y}, y)$
通过这个称为L的损失函数,来衡量预测输出值和实际值有多接近。
单次训练损失函数:
$\Large{L(\hat{y}, y) = -y\log(\hat{y}) - (1 - y)\log(1 - \hat{y})}$
在逻辑回归中用到的也是上方的损失函数
代价函数(Cost Function)
为了训练逻辑回归模型的参数参数𝑤和参数𝑏,我们需要一个代价函数,通过训练代价函数来得到参数𝑤和参数𝑏。
代价函数也叫做成本函数,也有人称其为全部损失函数。
损失函数是在单个训练样本中定义的,它衡量的是算法在单个训练样本中表现如何,为了衡量算法在全部训练样本上的表现如何,我们需要定义一个算法的代价函数。
算法的代价函数是对个 m 样本的损失函数求和,然后除以 m:
$\Large{J(w, b) = \frac{1}{m}\sum_{i=1}^{m}L\left(\hat{y}^{(i)}, y^{(i)})\right. = \frac{1}{m}\sum_{i=1}^{m}\left(-y^{(i)}log\hat{y}^{(i)}-(1-y^{(i)})log(1-\hat{y}^{(i)}))\right.}$
损失函数只适用于像这样的单个训练样本,而代价函数是参数的总代价,所以在训练逻辑回归模型时候,我们需要找到合适的$w$和$b$,来让代价函数$J$ 的总代价降到最低。
代价函数的解释
简洁的证明逻辑回归的损失函数为什么是这种形式。
回想一下,在逻辑回归中,需要预测的结果 $\hat{y}$, 可以表示为 $\hat{y} = \sigma{(wx + b)}$,$\sigma{}$ 是我们熟悉的 $S$ 型函数 $\sigma{(z)} = \sigma{(wx + b)} = 1 + e^{-z}$。
我们约定 $\hat{y} = p(y = 1 | x)$,即算法的输出 $\hat{y}$ 是给定训练样本 $x$ 条件下 $y$ 等于 1 的概率。
推导条件概率公式
换句话说,如果 $y = 1$,在给定训练样本 $x$ 条件下 $y = \hat{y}$;
反过来说,如果 $y = 0$,在给定训练样本 $x$ 条件下 $y = 1 - \hat{y}$,
因此,如果 $\hat{y}$ 代表 $y = 1$ 的概率,那么 $1 - \hat{y}$ 就是 $y = 0$ 的概率。
由上述推论可得出这两个条件概率公式:
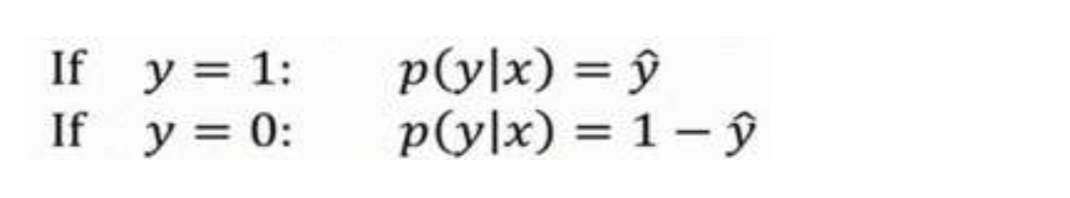
以下类似手写截图均来自吴恩达老师的深度学习课程
可将上述公式,合并成如下公式:
$$\Large{p(y | x) = \hat{y}^y(1 - \hat{y})^{(1 - y)}}$$
解释合并过程
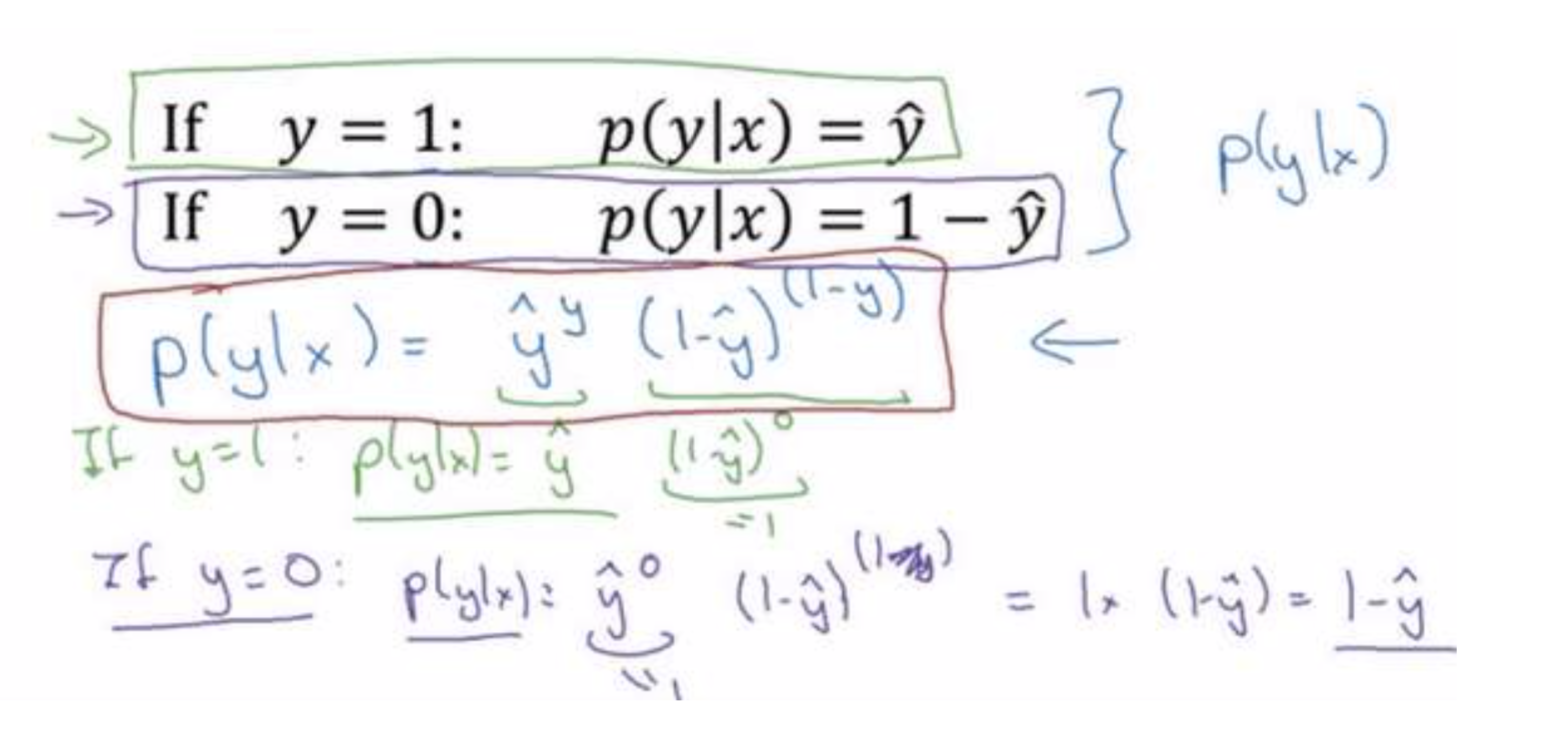
分别假设 $y = 1$,$y = 0$ 条件,对合并公式 $p(y | x) = \hat{y}^y(1 - \hat{y})^{(1 - y)}$ 进行计算,均可反推导出上述(2)中两个条件概率公式,反证(3)中合并公式就是 𝑝(𝑦|𝑥) 的完整定义。
进一步推导 logp,得到单个训练样本的损失函数
由于 log 函数是严格单调递增的函数,最大化 $log(p(y | x))$ 等价于最大化 $p(y | x)$ ,所以将$p(y | x)$带入公式后,计算 $p(y | x)$ 的 log 对数,就是计算 $log(\hat{y}^y(1 - \hat{y})^{(1 - y)})$,通过对数函数化简为:
$$\Large{logp = ylog\hat{y} + (1 - y)log(1 - \hat{y}) = -L(\hat{y}, y)}$$
这就是我们前面提到的损失函数 $L(\hat{y}, y)$ 的负数.
前面有一个负号的原因:当训练学习算法时,需要算法输出值的概率是最大的(以最大的概率预测这个值),然而在逻辑回归中我们需要最小化损失函数。
因此最小化损失函数与最大化条件概率的对数 $log(p(y | x))$ 关联起来了,上述公式就是单个训练样本的损失函数表达式。
推导到 m 个训练样本的整体训练的代价函数
其实就是将(5)中公式进行集合计算。
$\Large{P}$$($ labels in training set $)$ = $\Large{\prod{m}P(y^{(i)}|x^{(i)})}$
进一步推导
$\Large{logp = - \sum_{i = 1}^m L(\hat{y}^{(i)}, y^{(i)})}$
在统计学里面,有一个方法叫做最大似然估计,即求出一组参数,使这个式子取最大值,这样我们就推导出了前面给出的 logistic 回归的代价函数:
$\Large{J(w, b) = \sum_{i = 1}^m L(\hat{y}^{(i)}, y^{(i)})}$
由于训练模型时,目标是让成本函数最小化,所以我们不是直接用最大似然概率,要去 掉这里的负号,最后为了方便,可以对成本函数进行适当的缩放,我们就在前面加一个额外的常数因子 $\frac{1}{m}$,即可得到整体训练的代价函数。
$\Large{J(w, b) = \frac{1}{m}\sum_{i = 1}^m L(\hat{y}^{(i)}, y^{(i)})}$
计算图
计算图是什么
一个神经网络的计算,都是按照前向或反向传播过程组织的。
首先我们计算出一个新的网络的输出(前向过程),紧接着进行一个反向传输操作。后者我们用来计算出对应的梯度或导数。
计算图解释了为什么我们用这种方式组织这些计算过程。
举例说明
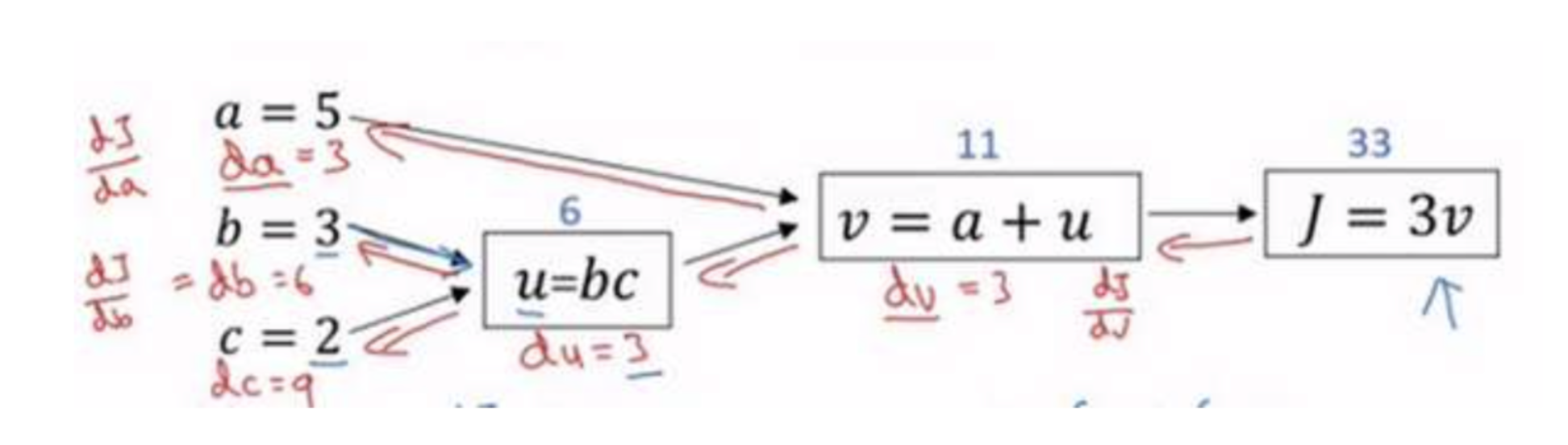
尝试计算函数$J = 3(a+bc)$, 分成3个步骤
- $u=bc$, 计算 $b$乘以$c$,把它储存在变量$u$中
- $v=a+u$
- $J=3v$
概括一下:计算图组织计算的形式是用蓝色箭头从左到右的计算
使用计算图求导数
进行反向红色箭头(也就是从右到左)的导数计算
$\frac{dJ}{du}=\frac{dJ}{dv}\frac{dv}{du}$, $\frac{dJ}{db}=\frac{dJ}{du}\frac{du}{db}$, $\frac{dJ}{da}=\frac{dJ}{du}\frac{du}{da}$
在反向传播算法中的术语,我们看到,如果你想计算最后输出变量的导数,使用你最关心的变量对𝑣的导数,那么我们就做完了一步反向传播。
当计算所有这些导数时,最有效率的办法是从右到左计算,跟着这个红色箭头走。
所以这个计算流程图,就是正向或者说从左到右的计算来计算成本函数J(你可能需要优化的函数)。然后反向从右到左是计算导数。
梯度下降
梯度下降法 (Gradient Descent)
梯度下降法可以做什么?
在你测试集上,通过最小化代价函数(成本函数)𝐽(𝑤, 𝑏)来训练的参数𝑤和𝑏
$\Large{J(w, b) = \frac{1}{m}\sum_{i=1}^{m}L\left(\hat{y}^{(i)}, y^{(i)})\right. = \frac{1}{m}\sum_{i=1}^{m}\left(-y^{(i)}log\hat{y}^{(i)}-(1-y^{(i)})log(1-\hat{y}^{(i)}))\right.}$
梯度下降法的形象化说明
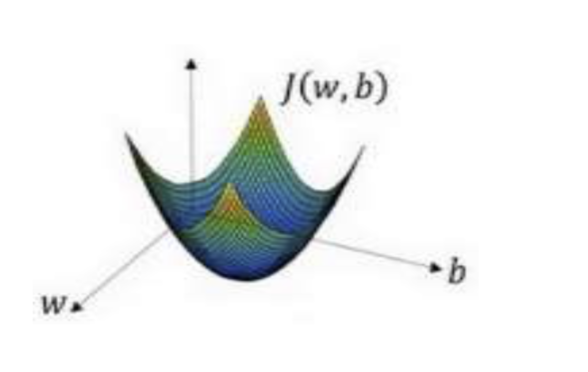
在这个图中,横轴表示你的空间参数𝑤和𝑏,在实践中,𝑤可以是更高的维度,但是为了 更好地绘图,我们定义𝑤和𝑏,都是单一实数,代价函数(成本函数)𝐽(𝑤, 𝑏)是在水平轴𝑤和 𝑏上的曲面,因此曲面的高度就是𝐽(𝑤, 𝑏)在某一点的函数值。我们所做的就是找到使得代价 函数(成本函数)𝐽(𝑤, 𝑏)函数值是最小值,对应的参数𝑤和𝑏。
以如图的小红点的坐标来初始化参数𝑤和𝑏。
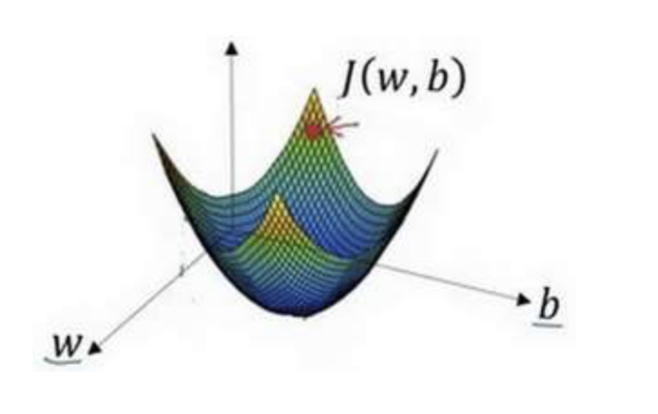
- 选出最陡的下坡方向,并走一步,且不断地迭代下去。
朝最陡的下坡方向走一步,如图,走到了如图中第二个小红点处。
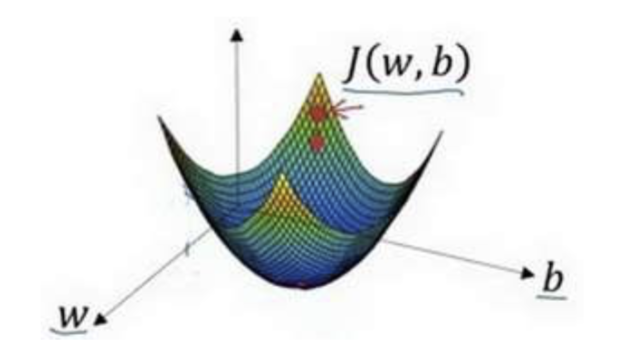
可能停在这里也有可能继续朝最陡的下坡方向再走一步,如图,经过两次迭代走到 第三个小红点处。

直到走到全局最优解或者接近全局最优解的地方。
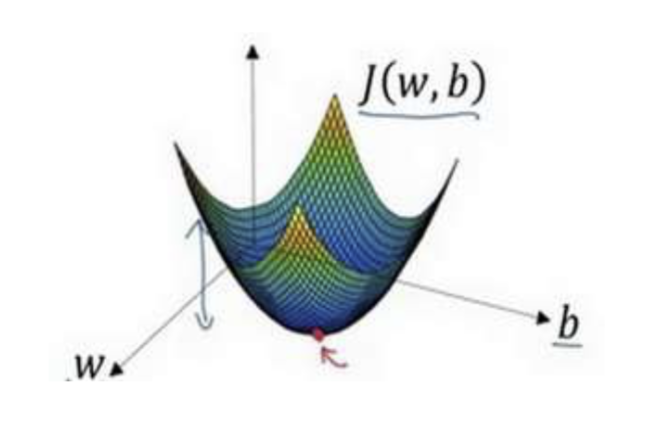
通过以上的三个步骤我们可以找到全局最优解,也就是代价函数(成本函数)𝐽(𝑤, 𝑏)这个凸函数的最小值点。
逻辑回归的梯度下降
- 假设样本只有两个特征𝑥1和𝑥2,为了计算𝑧,我们需要输入参数𝑤1、𝑤2 和𝑏,除此之外 还有特征值𝑥1和𝑥2。
因此𝑧的计算公式为: 𝑧 = 𝑤1𝑥1 + 𝑤2𝑥2 + 𝑏
回想一下逻辑回归的公式定义如下: 𝑦=𝑎=𝜎(𝑧) 其中𝑧=𝑤 𝑥+𝑏,𝜎(𝑧)=1+𝑒−𝑧
损失函数: $L(\hat{y}, y) = -y\log(\hat{y}) - (1 - y)\log(1 - \hat{y})$
代价函数: $J(w, b) = \frac{1}{m}\sum_{i = 1}^m L(\hat{y}^{(i)}, y^{(i)})$
假设现在只考虑单个样本的情况,单个样本的代价函数定义如下:
$L(a, y) = -y\log(a) - (1 - y)\log(1 - a)$
其中𝑎是逻辑回归的输出,𝑦 是样本的标签值。
这里先复习下梯度下降法,𝑤 和 𝑏 的修正量可以表达如下:
$$ w := w - a\frac{\partial{J(w, b)}}{\partial{w}}$$
$$ b := b - a\frac{\partial{J(w, b)}}{\partial{b}}$$
反向传播计算 𝑤 和 𝑏 变化对代价函数 𝐿 的影响
第一步反向推到
反向计算出代价函数𝐿(𝑎, 𝑦)关于𝑎的导数
通过微积分得到: $\frac{dL(a, y)}{da}= -\frac{y}{a} + \frac{(1 - y)}{(1 - a)}$
第二步反向推导
反向计算 dz,用 𝑑𝑧 来表示代价函数 𝐿 关于 𝑧 的导数 $\frac{dL}{dz}$,也可以写成 $\frac{dL(a, y)}{dz}$,这两种写法都是正确的。
因为 $\frac{dL(a, y)}{dz} = \frac{dL}{dz} = (\frac{dL}{da})\cdot(\frac{da}{dz})$, 已知 $\frac{da}{dz} = a \cdot(1-a)$,且 $\frac{dL}{da}= -\frac{y}{a} + \frac{(1 - y)}{(1 - a)}$,代入可得
$$\Large{dz = \frac{dL(a, y)}{dz} = \frac{dL}{dz} = (\frac{dL}{da})\cdot(\frac{da}{dz}) = (-\frac{y}{a} + \frac{(1 - y)}{(1 - a)}) \cdot a(1-a) = a - y}$$
最后一步反向推导
计算 𝑤 和 𝑏 变化对代价函数 𝐿 的影响,由上步推导已知 $dz = \frac{dL}{dz} = a - y$,所以对 w 和 b 求导可得
$ dw_1 = \frac{1}{m}\sum_i^m x_1^{(i)}(a^{(i)} - y^{(i)}) $
$ dw_2 = \frac{1}{m}\sum_i^m x_2^{(i)}(a^{(i)} - y^{(i)}) $
$ db = \frac{1}{m}\sum_i^m (a^{(i)} - y^{(i)}) $
单个样本的梯度下降算法
由上述反向传播推导,已得知多个样本下的梯度下降方法,在单个样本时,需要做的步骤为:
使用公式 $dz = a - y$ 计算 𝑑𝑧
使用 $dw_1 = x_1 \cdot dz $ 计算 $dw_1$, $dw_2 = x_2 \cdot dz $ 计算 $dw_2$, $db = dz $ 来计算 $db$
更新 $w_! = w_! - dw_1 $,更新 $w_2 = w_2 - dw_2 $,更新 $b = b - db $
这就是关于单个样本实例的梯度下降算法中参数更新一次的步骤。
网络向量化
我们已经了解了单个训练样本的损失函数,当使用编程进行计算多个训练样本的代价函数时,一般都会想到使用 loop 循环来计算。
但是在数学科学领域,训练一个模型可能需要非常大量的训练样本, 即大数据集,使用 loop 循环遍历的方式是十分低效的。
线性代数的知识起到了作用,我们可以通过将循环遍历的样本数据,进行向量化,更直接的、更高效的计算,提高代码速度,减少等待时间,达到我们的期望。
注意:虽然有时写循环(loop)是不可避免的,但是我们可以使用比如 numpy 的内置函数或者其他办法去计算。
前向传播向量化表示
$\Large{ Z = w^TX+b = np.dot(w.T, X) + b }$
$\Large{ A = \sigma{(Z)} }$
反向传播向量化表示
$\Large{ dZ = A - Y }$
$\Large{ dw = \frac{1}{m} * X \cdot dz^T }$
$\Large{ db = \frac{1}{m} * np.sum(dZ) }$
梯度下降更新参数
$\Large{ w := w - a * dw }$
$\Large{ b := b - a * db }$
神经网络训练过程
在深度学习中,我们一般都会使用第三方框架,如 TensorFlow,训练过程对我们来说是不可见的。
上面讲了很多的函数、以及其概念、作用,这些神经网络的”组件“,或者说,”组成部分“,如何串联起来呢?以及为什么一开始就会提到 ”前向传播“ 和 ”后向传播“ 这两个概念?
在一个神经网络的训练过程中,简化分为几步:
引入外部包
加载数据集
定义计算图
初始化参数,开始执行训练过程,执行计算图,一层层计算,直到计算到输出层,得到预估值、准确率、损失函数。(这是一个前向传播的过程)
对上次得到损失函数求导,使用梯度下降的方法从右向左对神经网络的每一层计算调参,直到计算到第一个隐含层,得到调整后的参数。(这是一个后向传播的过程)
在神经网络的训练中,每一次步长的训练中,都会先执行一次前向传播计算损失,再执行一次后向传播调整参数,交迭进行得到新的模型。
数据集训练完毕,得到训练完毕的模型的最终损失和准确率。